Resources

Question Source: https://leetcode.com/problems/search-in-a-binary-search-tree/

Iterative: O(log(n)) / O(1)

Intuition

Binary Search Trees have the property that all the children node (down to the bottom) to the left of the parent is smaller than the parent, and all the children node on the right of the parent is greater than the parent:

Education P1

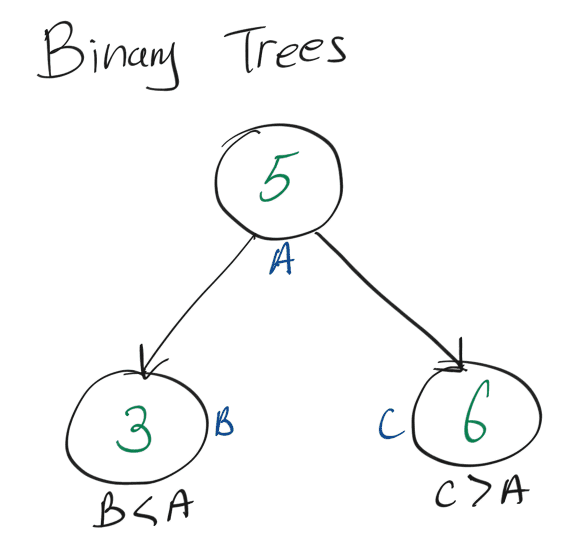
Since we are given the root of a binary tree, we can traverse the tree based on whether the value of the node is greater than or less than the target:

If target > node value, go to right child
If target < node value, go to left child
If target == node value, return the node
If the node becomes None then it means the target node does not exist, and return None

Big-O

In the worst case scenario, the time complexity for binary tree search is O(n) because the tree is unbalanced and looks like this:

In the above case, we have to traverse every node, so we traverse n times, and have O(n) runtime.

However, for a balanced binary tree like below:

           5
         /   \
        4     7
       / \   / \
      2   5 6   9

We have O(log(n)) runtime because we only have to traverse the height of the tree, which is log₂(n).

Code

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def searchBST(self, root, val):
        node = root
        while node != None:
            if node.val == val:
                print(node.val)
                return node
            elif val < node.val:
                node = node.left
            else:
                node = node.right
        return None

node1 = TreeNode(1,None,None)
node3 = TreeNode(3,None,None)
node2 = TreeNode(2,node1,node3)
node7 = TreeNode(7,None,None)
node4 = TreeNode(4,node2,node7)

s = Solution()
print(s.searchBST(node4,2))

Here is a more condensed refactor

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def searchBST(self, root, val):
        node = root
        # combine the if statement into while loop
        while node != None and node.val != val:
            # ternary operater
            node = node.left if val < node.val else node.right
        return node

node1 = TreeNode(1,None,None)
node3 = TreeNode(3,None,None)
node2 = TreeNode(2,node1,node3)
node7 = TreeNode(7,None,None)
node4 = TreeNode(4,node2,node7)

s = Solution()
print(s.searchBST(node4,2))

Recursion: O(n) / O(n)

It's possible to solve using recursion, but it's less intuitive (for me), and it uses more space.

Because the code must recurse through the whole tree, the recursion stack takes up on average O(log(n)) space and at worst O(n) space. See above explanation.

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def searchBST(self, root, val):
        node = root
        if node.val == val:
            return node
        if val > node.val:
            return self.searchBST(node.right, val)
        else:
            return self.searchBST(node.left, val)

node1 = TreeNode(1,None,None)
node3 = TreeNode(3,None,None)
node2 = TreeNode(2,node1,node3)
node7 = TreeNode(7,None,None)
node4 = TreeNode(4,node2,node7)

s = Solution()
print(s.searchBST(node4,2)) # node2

Table of Contents