Resources

Question Source: Leetcode

O(n²) Runtime Solutions

All the solutions below unfortunately require iterating through all the possible combinations in the worst case scenario, resulting in O(n²) time complexity, which is not ideal.

Decision Tree - Top Down Recursion

For every person, we can either send them to City A or City B. But there is a limit for each city that the capacity is only N/2.

We can make a decision tree and sum up the total cost at all the leaf nodes. Then, choose the leaf node with the least total cost.

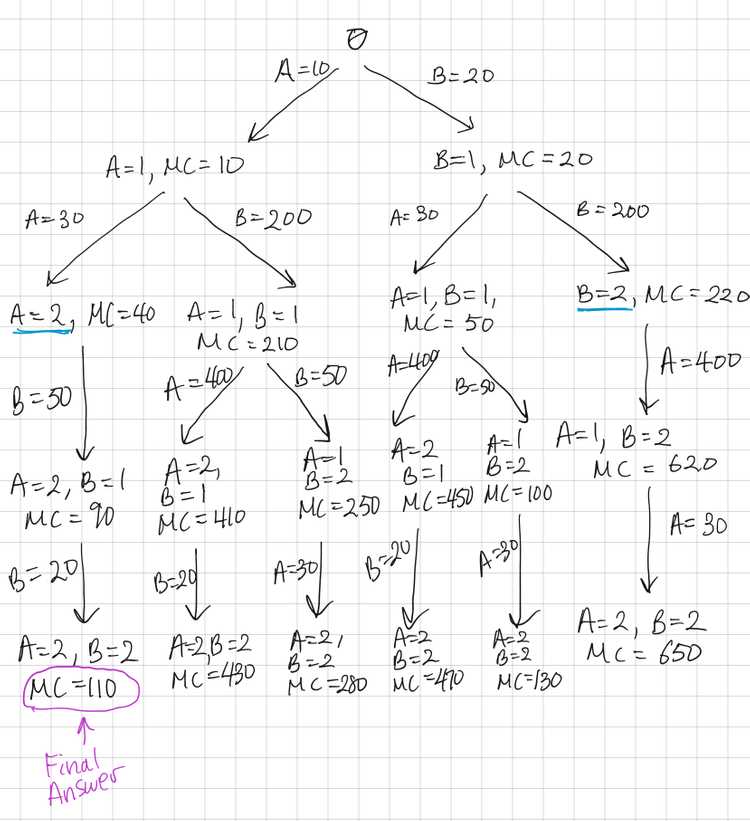
Find all possible combinations

This is essentially the same approach as the decision tree, but instead we find all possible combinations of City A and City B where N/2 people are assigned to each city. Then we add up the total cost of each combination and choose the lowest cost.

Assign cheapest city, then re-assign

If there were no limits on the capacity for a city, then we would simply take the lowest cost city for every person. This is how we get the Cities array below. 0 means assign to City A, and 1 means assign to City B.

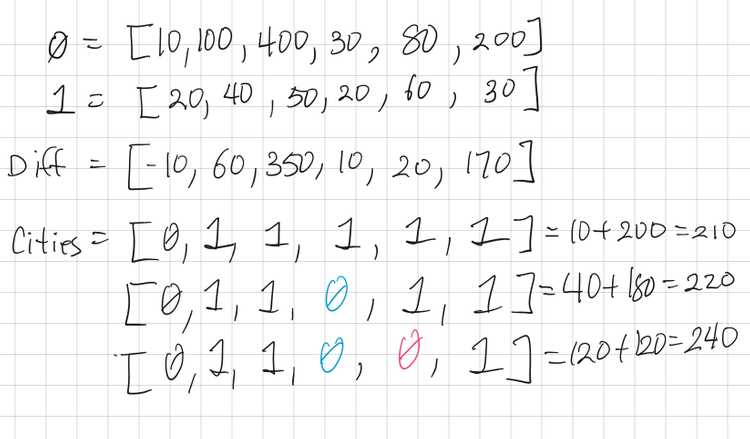
But if through that approach we are over-capacity for one city X, then we need to remove people from city X to the other city. The rule for doing this will be that we choose the minimum cost difference.

In the above example, we have too many people in City B. In this case, we need to move people out of City B, and into City A. We want to remove as much cost as possible, and add as little cost as possible. This means we want to maximize the value of (B - A).

Diff array shows the difference between A - B. So, since it’s the oppose of what we want, we want to choose the smallest values from Diff to put into City A.

In this case, the smallest Diff values are -10, 10 and 20. -10 is already in our Cities array, 10 and 20 need to be moved to City A, which are indexes 3 and 4.

Dynamic Programming

A dynamic programming solution can be derived from the approach of the above 2 solutions. And the runtime is still O(n²) at best.

Some good reads about a DP solution for this problem:

• Youtube: Two City Scheduling | LeetCode 1029 | C++, Java, Python
• Leetcode Discussions | A dynamic programming solution. No code just explanation.
• Leetcode Discussions | Java DP - Easy to Understand

Sorting / Greedy: O(nLogn) / O(n)

Like in the above solutions, we find the Diff between each city, but this time, we sort the Diff array from least to greatest.

Since our Diff array is the value of A-B, the values that are smallest are the ones that should be assigned to City A, and the values that are largest should be assigned to City B.

When we create Diff, we should also include the index of the value, so that we remember which “person” it is after the sort. We can use tuples for that: (diff, idx)

The final sorted array will look like below, and the first N/2 will be City A, while the latter half is City B.

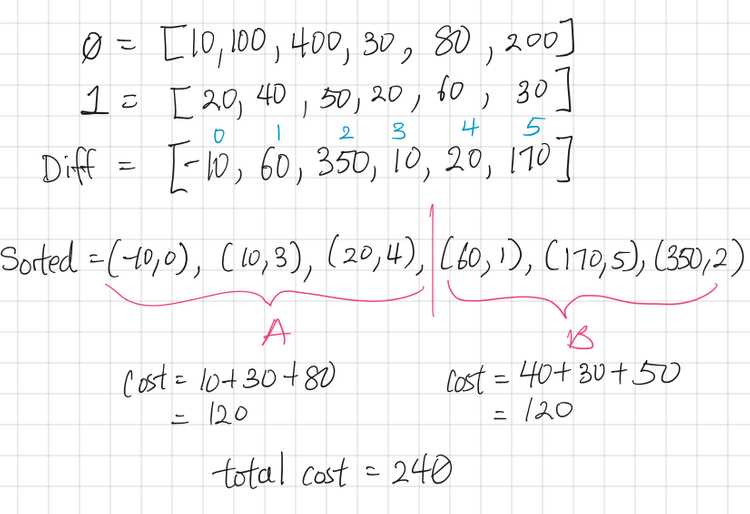
To get the final cost, we have to use the index saved in each tuple to get the cost and then add them all up.

See a more formal proof for the Greedy Solution

class Solution:
    def twoCitySchedCost(self, costs):
        """
        costs type: List[List[int]]
        rtype: int
        """
        diff = [None] * len(costs)
        for i in range(len(costs)):
            val = costs[i][0] - costs[i][1]
            diff[i] = (val,i)
        # print(diff)

        diff.sort()
        # print(diff)

        cost = 0
        for i in range(len(diff)):
            idx = diff[i][1]
            if i < len(diff) / 2:
                cost += costs[idx][0]
            else:
                cost += costs[idx][1]
            # print(cost)
        return cost

s = Solution()
print(s.twoCitySchedCost([[10, 20], [100, 40], [400, 50], [30, 20],[80,60],[200,30]])) # 240
print(s.twoCitySchedCost([[10,20],[30,200],[400,50],[30,20]])) # 110

Using Lambda to Sort: O(n*Logn) / O(1)

The above solution has a space complexity of O(n) because we must store the Diff array. This can be improved upon by using lambda to reduce space to O(1).

class Solution:
    def twoCitySchedCost(self, costs: List[List[int]]) -> int:
        # Sort by a gain which company has 
        # by sending a person to city A and not to city B
        costs.sort(key = lambda x : x[0] - x[1])
        
        total = 0
        n = len(costs) // 2
        # To optimize the company expenses,
        # send the first n persons to the city A
        # and the others to the city B
        for i in range(n):
            total += costs[i][0] + costs[i + n][1]
        return total