ChunYu's Algorithm Library
- 0. 1/0 Knapsack Problem
- 0. Bike Rental Scheduling
- 0. Max Sum Increasing Subsequence
- 1. Two Sum
- 19. Remove Nth Node From End of List
- 35. Insert Search Position
- 45. Jump Game II
- 53. Maximum Subarray
- 63. Unique Paths II
- 70. Climbing Stairs
- 72. Edit Distance (Levenshtein Distance)
- 75. Sort Colors (Dutch National Flag)
- 78. Subsets (Power Set)
- 136. Single Number
- 141. Linked List Cycle
- 150. Evaluate Reverse Polish Notation
- 160. Intersection of Two Linked Lists
- 169. Majority Element
- 200. Number of Islands
- 210. Course Schedule II
- 215. Kth Largest Element in an Array
- 226. Invert Binary Tree
- 231. Power of Two
- 234. Palindrome Linked List
- 237. Delete a Node in a Linked List
- 279. Perfect Squares
- 322. Coin Change
- 323. Number of Connected Components in an Undirected Graph
- 344. Reverse a String
- 380. Insert Delete GetRandom O(1)
- 383. Ransom Note
- 392. Is Subsequence
- 406. Queue Reconstruction by Height
- 417. Pacific Atlantic Water Flow
- 468. Validate IP Address
- 490. The Maze
- 509. Fibonacci Number
- 518. Coin Change II
- 520. Detect Capital
- 528. Random Pick with Weight
- 690. Employee Importance
- 700. Search in a Binary Search Tree
- 703. Kth Largest Element in a Stream
- 705. Design Hashset
- 706. Design Hashmap
- 733. Flood Fill
- 912. Sort an Array
- 933. Number of Recent Calls
- 994. Rotting Oranges
- 1029. Two City Scheduling
- 1431. Kids with Greatest Number of Candies
- 1436. Destination City
- 1437. Check If All 1's are at Least Length K Places Away
- 1446. Consecutive Characters
- 1447. Simplified Fractions
- .
322. Coin Change
Last Updated: 2020.05.31
Table of Contents
Resources
Question Source: https://leetcode.com/problems/coin-change
Dynamic Programming (Bottom-Up)
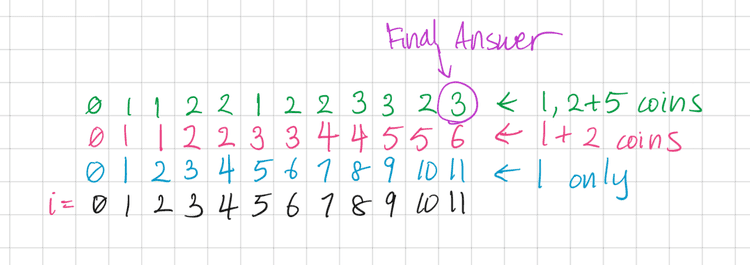
May 31, 2020
Runtime: O(a*c) where a = amount, c = number of coins
Space: O(a) where a = amount
class Solution:
def coinChange(self, coins, amount):
"""
For a given set of coin denomations, return the smallest number of coins that can be used to add up to a given target amount.
coins type: List[int]
amount type: int
rtype: int
"""
ways = [float('inf')]*(amount+1)
ways[0] = 0
for c in coins:
for i in range(1,amount+1):
if i >= c:
ways[i] = min(ways[i],ways[i-c]+1)
# print(ways)
if ways[-1] == float('inf'):
return -1
return ways[-1]
s = Solution()
print(s.coinChange([1],2)) # 2
print(s.coinChange([2],1)) # -1
print(s.coinChange([2],3)) # -1
print(s.coinChange([2,3],4)) # 2
print(s.coinChange([1,2,5],11)) # 3
print(s.coinChange([2, 5, 10, 1],27)) # 4
print(s.coinChange([1,2,5],100)) # 20
print(s.coinChange([431,62,88,428],9084)) # 26Recursion w/ Memoization (Top-Down)
Good explanation: Back-to-Back SWE

BFS Using Dictionary - May 31, 2020
Runtime: O(a*c) where a = amount, c = number of coins (forks in the tree)
Space: O(a*c) where a = amount, c = number of coins (forks in the tree)
class Solution:
def coinChange(self, coins, amount):
"""
For a given set of coin denomations, return the smallest number of coins that can be used to add up to a given target amount.
coins type: List[int]
amount type: int
rtype: int
"""
if amount == 0:
return 0
levels = {1:[]}
visited = set()
cur_level = 1
found = False
for c in coins:
levels[1].append(c)
# print(levels)
while found == False:
for item in levels[cur_level]:
if item in visited:
continue
if item == amount:
return cur_level
elif item > amount:
continue
else:
if (cur_level + 1) not in levels:
levels[cur_level+1]=[]
for c in coins:
levels[cur_level+1].append(item + c)
# print(levels)
visited.add(item)
cur_level += 1
if cur_level not in levels:
return -1
s = Solution()
print(s.coinChange([1],2)) # 2
print(s.coinChange([2],1)) # -1
print(s.coinChange([2],3)) # -1
print(s.coinChange([2,3],4)) # 2
print(s.coinChange([1,2,5],11)) # 3
print(s.coinChange([2,5,10,1],27)) # 4
print(s.coinChange([1,2,5],100)) # 20
print(s.coinChange([431,62,88,428],9084)) # 26Using BFS Queue
The above dictionary solution can also be implemented with a Queue, but it looks like the space & time complexity has no improvement.
Runtime: O(a*c) where a = amount, c = number of coins (forks in the tree)
Space: O(a*c) where a = amount, c = number of coins (forks in the tree)
References
- Top-Down Approach: Back-to-Back SWE